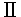 DINDICATION OF CONTRADICTION OF SPECIAL RELATIVITY AND INTRODUCTION OF AN UNKNOWN PHYSICAL QUANTITY : A DEPTH VELOCITY VECTOR DINDICATION OF CONTRADICTION OF SPECIAL RELATIVITY AND INTRODUCTION OF AN UNKNOWN PHYSICAL QUANTITY : A DEPTH VELOCITY VECTOR
|
|
@To detect by an experiment the difference between the spaces in the rocket
a and b presented in the introduction, we consider a thought experiment
below.
@[Thought experiment 2]
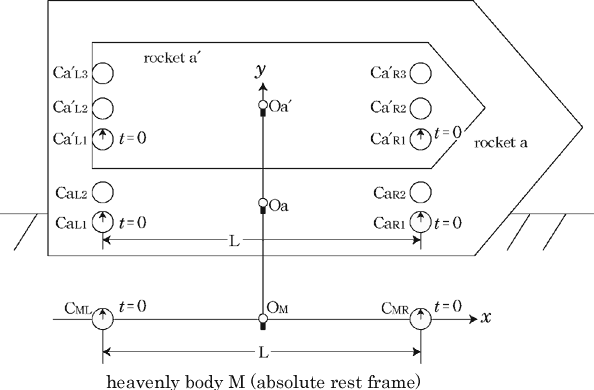
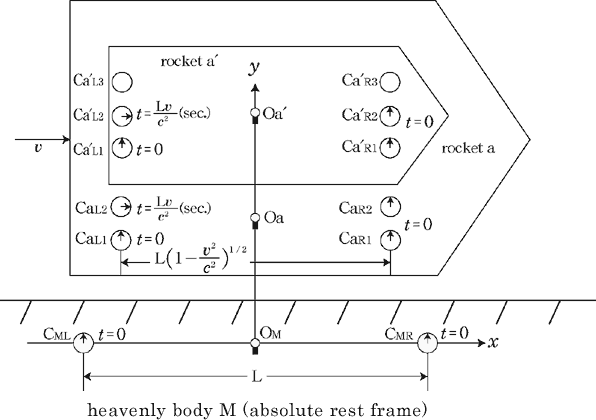
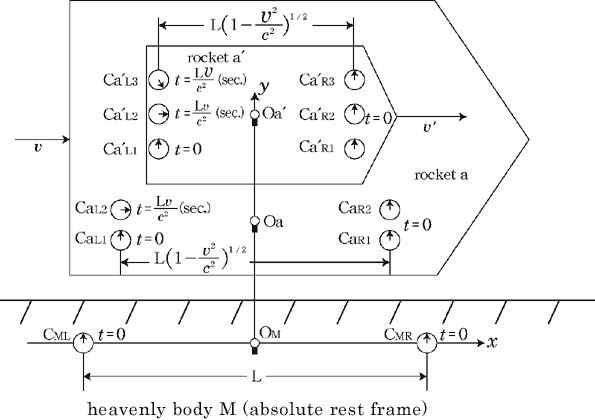
@Let us consider the condition where the rocket a is at rest along the
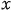 axis on the heavenly body M in Fig.1a, and another rocket a axis on the heavenly body M in Fig.1a, and another rocket a in a is at rest.(see Fig.2) in a is at rest.(see Fig.2)
|
 |
|
|
@In the center of the rockets a and a the light sources the light sources  and and 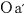 are set, which share the are set, which share the 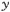 axis with the light source axis with the light source 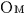 , installed on the origin of the , installed on the origin of the 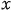 - -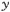 axis on M. At the six points on M, in a and a axis on M. At the six points on M, in a and a , twelve clocks of the same kind are placed at equal distance , twelve clocks of the same kind are placed at equal distance 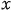 }L/2 from the light sources, the clocks which work exactly at the same tempo when at rest: one clock is placed at each end on M, two clocks at each end in a and three clocks at each end in a }L/2 from the light sources, the clocks which work exactly at the same tempo when at rest: one clock is placed at each end on M, two clocks at each end in a and three clocks at each end in a . The clock placed at the point . The clock placed at the point 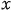 |L/2 on |L/2 on 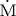 is expressed as is expressed as 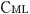 which means ethe which means ethe 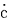 lock at the lock at the 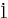 eft side of the light sourcef, while the one placed at the point eft side of the light sourcef, while the one placed at the point 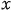 =L/2 is expressed as =L/2 is expressed as 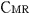 meaning ethe meaning ethe 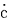 lock at the lock at the 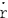 ight side of the sourcef. In the same way, the four clocks in a are expressed as ight side of the sourcef. In the same way, the four clocks in a are expressed as  , , 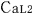 , , 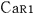 , , 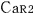 . And the six clocks in a . And the six clocks in a are expressed as are expressed as 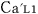 , , 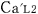 , , 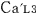 , , 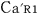 , , 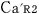 , , 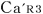 . .
@Then we set three pairs of clocks (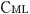 and and 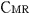 , , and and 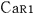 , ,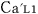 and and 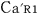 ) using the way of clock settings which was used by Einstein when he constructed special relativity. ) using the way of clock settings which was used by Einstein when he constructed special relativity.
@In this case, M is at rest relative to the center of the gravity and is regarded as ethe absolute rest framef. And the spreads of the lights 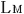 , , 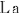 and and 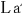 emitted from the three sources which are at rest on M are thought to be
isotropic relative to the observer emitted from the three sources which are at rest on M are thought to be
isotropic relative to the observer 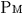 . .
@Therefore, those six clocks can be said to agree with one another in
the absolute sense.
@The next clock setting is about 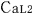 and and 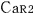 in the rocket a, which begins to move at the uniform velocity in the rocket a, which begins to move at the uniform velocity  relative to M, and about relative to M, and about 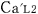 and and 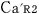 in the rocket a in the rocket a , which is still at rest in a.(see Fig.3) , which is still at rest in a.(see Fig.3)
|
|
|
|
|
@Since these two pairs of clocks are set in the same way, we consider
the clock setting of 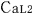 and and 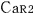 . .
@Let us consider the case in which an observer  , who is at rest on the heavenly body M, measures the time required for the light , who is at rest on the heavenly body M, measures the time required for the light  emitted from the source emitted from the source  to reach to reach  . When . When 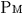 measures the distance between measures the distance between 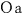 and and 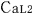 , which is L/2 in the rocket, it is , which is L/2 in the rocket, it is 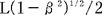 @( @(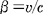 ) because the rocket a contracts in the moving direction at the rate of ) because the rocket a contracts in the moving direction at the rate of 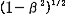 . Therefore, by . Therefore, by  's clock, the time 's clock, the time 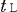 required for required for 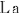 to reach to reach 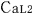 is@ is@
|
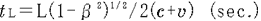
|
i Pj Pj
|
|
|
@On the other hand, the time 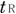 required for required for 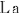 to reach to reach 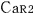 is is
|
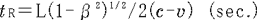
|
i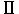 Qj Qj
|
|
|
@But, the clock ticks at the rate of 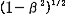 : 1, compared with : 1, compared with 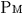 's clock. Thus, from 's clock. Thus, from 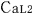 and and 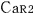 , , 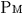 observes the time difference observes the time difference 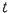 required for required for 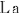 to reach to reach 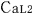 and and 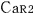 , ,
|
|
i Rj Rj
|
|
|
@That is, 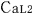 is is 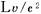 sec. fast compared with sec. fast compared with 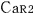 . .
@The same is true with the time difference between 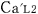 and and 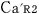 . What we have to notice, however, is it is when . What we have to notice, however, is it is when 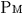 measures the time that measures the time that 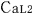 and and 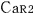 disagree with each other. For the observer disagree with each other. For the observer 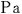 in the rocket a, these two clocks agree with each other. in the rocket a, these two clocks agree with each other. 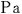 can not discuss the absolute time difference between them as it is. can not discuss the absolute time difference between them as it is.
@Then, as a next operation, a time adjustment 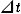 is made so that is made so that 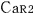 and and 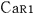 agree, which usually do not. agree, which usually do not.
@In addition, the same adjustment 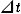 is made about is made about 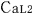 .(Of course we do not really have to make the clocks agree. Calculational
adjustment is enough) .(Of course we do not really have to make the clocks agree. Calculational
adjustment is enough)
@When 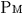 observes this situation, observes this situation, 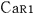 , , 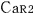 and and  agree with one another, while agree with one another, while 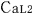 is is 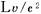 sec. fast. Therefore, when the observer in the rocket a ( sec. fast. Therefore, when the observer in the rocket a (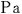 ) compares ) compares  with with 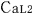 , the latter is , the latter is 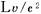 sec. fast. This agrees with the prediction of special relativity. sec. fast. This agrees with the prediction of special relativity.
@When the same clock setting and time adjustment are made about 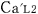 and and 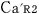 in the rocket a in the rocket a the observer the observer 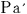 will find that will find that 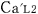 is is 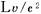 sec. fast comparing sec. fast comparing 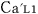 with with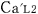 . .
@Next, we make a clock setting about 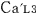 and and 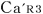 when the rocket a when the rocket a in the rocket a begins to move at the uniform velocity in the rocket a begins to move at the uniform velocity  '. (see Fig.4) '. (see Fig.4)
|
 |
|
|
|
@Now, we regard the velocity of a observed by observed by 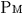 as as 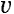 , and when , and when 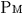 observes the time difference observes the time difference 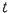  between between 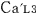 and and 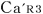 , ,
|
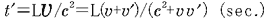
|
i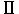 Sj Sj
|
|
|
@as is clear from the previous consideration.
@[From the theory of relativity, 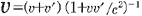 ] ]
@ Then, as a next operation, a time adjustment 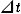  is made in order to make is made in order to make 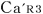 agree with agree with 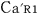 and and 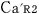 . .
|
|
@In addition, the same adjustment 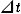  is made about is made about 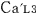 . .
@When this situation is observed by 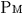 , , 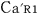 , , 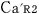 , , 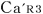 and and 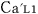 agree with one another. But agree with one another. But 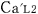 is is 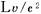 sec. fast, and sec. fast, and 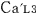 is is 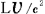 sec. fast relative to these four clocks. sec. fast relative to these four clocks.
@Consequently, when the observer 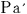 in the rocket a in the rocket a compares compares 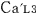 with with 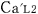 , the former is , the former is
|
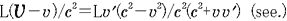
|
i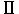 Tj Tj
|
|
|
@fast relative to the latter. This result contradicts the prediction of
special relativity.
@According to the supposition of ethe principle of relativityf, which
was used when special relativity was constructed, inertia1 frames moving
relatively are equal and so the laws of physics must be the same in every
inertial frame.@Thus, if the time difference between  and and 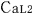 in the rocket a (moving at the uniform velocity in the rocket a (moving at the uniform velocity  above the heavenly body M ) is above the heavenly body M ) is 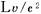 sec., the time difference between sec., the time difference between 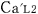 and and 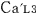 in the rocket a in the rocket a (moving at the uniform velocity (moving at the uniform velocity   in the rocket a) must be in the rocket a) must be 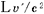 sec. sec.
@But the thought experiment in this paper does not produce such an result.
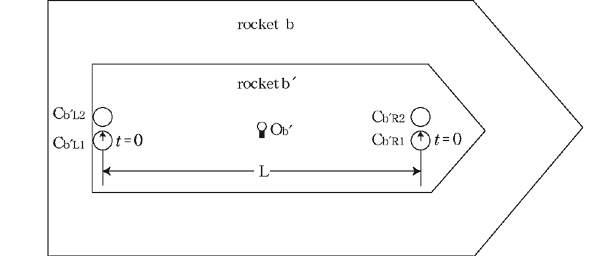
@By the way, let us consider the clock settings of the four clocks in a rocket b which is in the rocket b in Fig.1b : which is in the rocket b in Fig.1b : 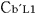 , , 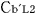 , ,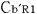 and and 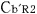 . (See Fig.5) . (See Fig.5)
|
|
|
Fig.5@In the rocket b(Fig.1b) the rocket bis at rest.
When the clock setting is made about 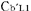 and and 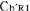 , they agree in the absolute sense. , they agree in the absolute sense.
|
|
|
@The distance between 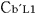 , , 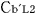 and and 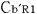 , , 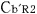 is L. The light source is L. The light source 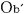 is at the center. is at the center.
@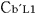 and and 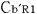 are set when the rocket b are set when the rocket b is at rest in the rocket b. In this case, the light is at rest in the rocket b. In this case, the light 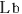 (emitted from the source in b (emitted from the source in b ) isotropically spreads a priori, and so we can say that ) isotropically spreads a priori, and so we can say that 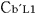 and and 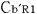 agree with each other in the absolute sense. agree with each other in the absolute sense.
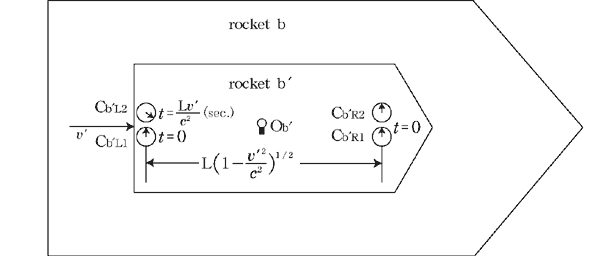
@Next, a clock setting about 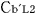 and and 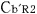 in the rocket b in the rocket b moving at the uniform velocity moving at the uniform velocity   in the rocket b.(see Fig.6) in the rocket b.(see Fig.6)
|
|
|
|
|
@When the observer in b (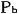 ) tells the time difference between these two clocks, ) tells the time difference between these two clocks, 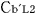 is is 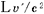 sec. fast relative to sec. fast relative to 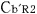 , as is clear from the previous consideration. , as is clear from the previous consideration.
@So, to make 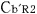 agree with agree with 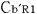 , a certain time adjustment , a certain time adjustment 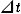 " is made. And the same adjustment " is made. And the same adjustment 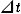 " is made about " is made about 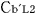 . .
@When 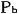 observes this situation, observes this situation, 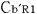 , , 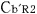 and and 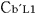 agree with one another, while agree with one another, while 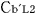 is is 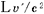 sec. fast relative to them. sec. fast relative to them.
@Consequently, as a matter of course, when the observer 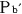 in the rocket b in the rocket b compares compares 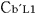 with with 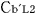 , the latter is , the latter is 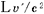 sec. fast relative to the former. sec. fast relative to the former.
@This result agrees with the prediction of special relativity.
@As for the time difference Eq.( 5) between 5) between 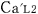 and and 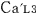 , which is compared in the same way, however, the prediction does not agree
with that. , which is compared in the same way, however, the prediction does not agree
with that.
@The correspondence of clock settings between these four clocks (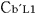 , , 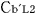 , , 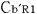 , , 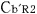 ) and the clocks( ) and the clocks(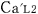 , , 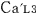 , , 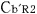 , , 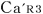 ) in the rocket a ) in the rocket a is as follows: is as follows:
|
|
|
Clocks in the rocket a( Fig.4 )
|
 |
*@clocks whose times are set when the rocket ais moving at a uniform
velocity  in the rocket a in motion. in the rocket a in motion.
|
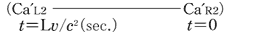 |
*@clocks whose times are set when the rocket a is at rest in the rocket
a in motion.
|
|
|
Clocks in the rocket b( Fig.6 )
|
 |
*@clocks whose times are set when the rocket bis moving at a uniform velocity  in the rocket b in motion. in the rocket b in motion.
|
 |
*@clocks whose times are set when the rocket bis at rest in the rocket
a in motion.
|
|
|
|
@From eThought experiment 2f, we have presented the way to detect the
difference of physical state between the inside space of the rocket a (see
Fig.1a) and the rocket b. (see Fig.1b)
@Now, what makes the time difference between 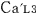 and and 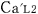 disagree with the prediction of special relativity? disagree with the prediction of special relativity?
@To explain the cause, we only have to think the space in the rocket a
is moving at ea certain velocity  f relative to some frame of reference. f relative to some frame of reference.
@However. ethe absolute rest spacef does not exist in the real physical
space. So it is impossible to regard ea certain velocity' as a velocity
relative to such a frame of reference.
@Then, this paper supposes that the physical space has a double layer.
@That is, we suppose an imaginary rest space | a depth rest space | in the depth of the real physical space, and suppose that the space in the rocket a, in which the spread of light is thought anisotropic, is moving at the velocity  relative to a depth rest space. In this case, we define that the space in the rocket a has a depth velocity vector relative to a depth rest space. In this case, we define that the space in the rocket a has a depth velocity vector  . (see Appendix) . (see Appendix)
@On the other hand, the space in the rocket b, in which the spread of light is thought isotropic, does not have a depth velocity vector.
@However, a depth rest space is not a real space. It is an imaginary one
which is introduced in order to describe ethe extent of the space dragging
effect by mass' with an unknown physical quantity : a depth velocity vector.
If we suppose the light spreads isotropically relative to each point in
this rest space, we can understand the speed of light does not depend on
the velocity of the light source. As for a depth velocity vector, the physical
space itself does not have it. It is a vector whose start point is a depth
rest space and the end is the real physical space.
@Now, let us calculate the magnitude of a depth velocity vector introduced
in the consideration above.
@In this paper, the magnitude is calculated from the time difference between 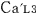 and and 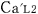 ( (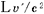 sec.) predicted by special relativity, and Eq.( sec.) predicted by special relativity, and Eq.(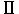 5 ) predicted in this paper. Generally speaking, however., the direction of a vector is not clear. So the component of its direction of 5 ) predicted in this paper. Generally speaking, however., the direction of a vector is not clear. So the component of its direction of 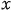 axis is regarded as axis is regarded as 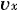 ( (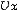 >0). >0).
@In addition, we define 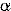 as below : as below :
|
|
@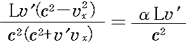
@From this, we obtain
|
i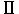 Uj Uj
|
|
@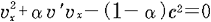 |
i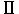 Vj Vj
|
|
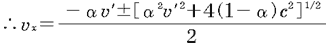
|
i Wj Wj
|
|
|
@The case we deal with is 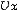 >0, so omit the minus solution,C >0, so omit the minus solution,C
|
@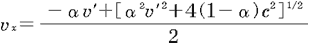
|
i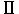 Xj Xj
|
|
|
@Now, we can get the component of a depth velocity vector in 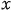 axis. If the same experiment is made about the direction of axis. If the same experiment is made about the direction of 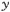 axis and axis and 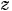 axis, we can get the magnitude of axis, we can get the magnitude of 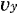 , and , and 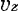 . .
@Therefore, we can get the magnitude of a depth velocity vector by synthesizing
the components of these three directions.
|




