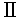 .特殊相対論の矛盾の指摘と未知の物理量,深層速度ベクトルの導入 .特殊相対論の矛盾の指摘と未知の物理量,深層速度ベクトルの導入
|
|
序論にて提示したロケットa,b内の空間の状態の相違を実験によって検出するため,次の思考実験について考える.
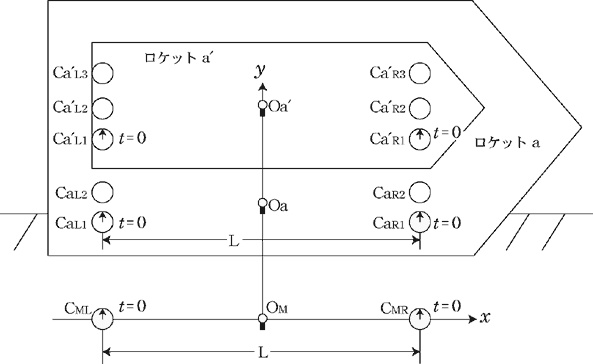
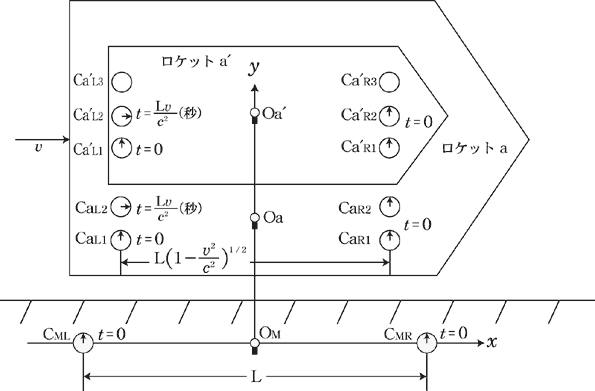
思考実験2…図1aの天体M上の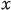 軸に沿ってロケットaが静止していて,そのロケット内に別のロケットa 軸に沿ってロケットaが静止していて,そのロケット内に別のロケットa が,同様に静止している状況を考える.(図2参照) が,同様に静止している状況を考える.(図2参照)
|
 |
|
天体M「絶対静止系」
|
|
図2.
|
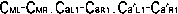 の時刻合わせ. の時刻合わせ.
|
|
6個の時計は,絶対的な意味で合っている.
|
|
|
ロケットa,a 内の中心には光源 内の中心には光源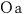 , ,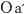 が設置されていて,これらは天体M上の が設置されていて,これらは天体M上の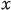 , ,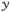 軸の交点に設置された光源 軸の交点に設置された光源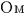 と と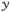 軸を共有しているものとする. 軸を共有しているものとする.
さらに,天体M,ロケットa,a の の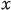 軸の= 軸の=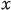 ±L/2,の6地点には静止時において正確に同じテンポで時を刻む同種の時計が,全部で12個設置してある. ±L/2,の6地点には静止時において正確に同じテンポで時を刻む同種の時計が,全部で12個設置してある.
すなわち,M上の2地点にはそれぞれ1個ずつの計2個,ロケットa内の2地点にはそれぞれ2個ずつの計4個,ロケットa 内の2地点にはそれぞれ3個ずつの計6個の時計が設置してある. 内の2地点にはそれぞれ3個ずつの計6個の時計が設置してある.
そして,天体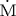 の の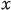 =-L/2,の地点に置かれた時計( =-L/2,の地点に置かれた時計(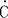 lock)を光源の左( lock)を光源の左(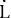 eft)の時計という意味で, eft)の時計という意味で,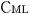 と表示し, と表示し,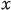 =L/2の地点に置かれた時計を光源の右( =L/2の地点に置かれた時計を光源の右(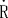 ight)の時計という意味で, ight)の時計という意味で,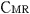 と表示する. と表示する.
また,ロケットa内の左右の4個の時計を , , 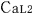 , 及び, , 及び, 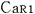 , , 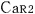 と表示し,ロケットa と表示し,ロケットa 内の左右の6個の時計を 内の左右の6個の時計を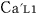 , ,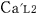 , ,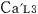 ,及び, ,及び,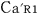 , , 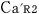 , , 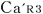 と表示する. と表示する.
そして,それらの時計の内で,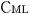 と と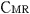 , , と と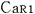 , ,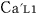 と と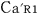 という対をなす3組の時計の時刻を,アインシュタインが特殊相対論を構築する際に用いた時刻合わせの方法を使って合わせる. という対をなす3組の時計の時刻を,アインシュタインが特殊相対論を構築する際に用いた時刻合わせの方法を使って合わせる.
この場合,宇宙の重心に対して静止していて,「絶対静止系」と考えられる天体M上に静止している3つの光源から放出された光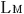 , ,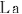 , ,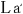 は,観測者 は,観測者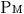 に対して等方的に伝播すると考えられるので,この方法によって合わせた6個の時計は,絶対的な意味で合っているといえる. に対して等方的に伝播すると考えられるので,この方法によって合わせた6個の時計は,絶対的な意味で合っているといえる.
さて,次の時刻合わせは,天体Mに対して速度 で等速度運動を始めたロケットa内の時計 で等速度運動を始めたロケットa内の時計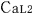 , ,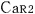 とロケットa内に依然として静止しているロケットa とロケットa内に依然として静止しているロケットa 内の時計 内の時計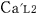 , ,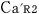 について行なう. について行なう.
これら2組の時刻合わせの方法は同様であるから,ここではロケットa内の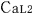 , ,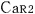 の時刻合わせについて考察する.(図3参照) の時刻合わせについて考察する.(図3参照)
|
|
|
天体M「絶対静止系」
|
|
図3.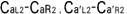 の時刻合わせ. の時刻合わせ.
|
|
この図では,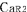 の時刻を の時刻を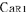 の時刻と一致させるために必要な時間調整を の時刻と一致させるために必要な時間調整を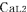 にも同様に行なっている.また にも同様に行なっている.また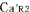 の時刻を の時刻を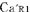 の時刻と一致させるために必要な時間調整を の時刻と一致させるために必要な時間調整を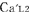 にも同様に行なっている. にも同様に行なっている.
|
|
いま,光源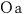 から放出された光 から放出された光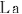 が,ロケット後方の時計 が,ロケット後方の時計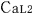 に到着するまでの時間を天体M上に静止している観測者 に到着するまでの時間を天体M上に静止している観測者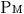 から測定した場合を考える. から測定した場合を考える.
ロケット内で,L/2,の距離があった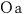 と と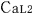 の距離を の距離を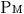 が測定すると,ロケットは進行方向に, が測定すると,ロケットは進行方向に,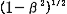 (ただし, (ただし,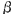 = = / /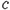 )の割合で収縮しているから, )の割合で収縮しているから, 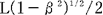 . .
従って,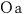 から放出された光 から放出された光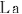 が, が,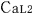 に到着するのに要する時間 に到着するのに要する時間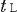 は, は,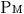 の時計で, の時計で,
|
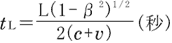
|
(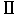 1) 1)
|
|
|
一方,光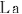 が が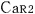 に到着するのに要する時間 に到着するのに要する時間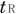 は, は,
|
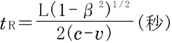
|
(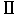 2) 2)
|
|
|
しかし,ロケット内の時計は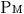 の時計に比べて, の時計に比べて,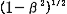 :1,の割合で時を刻むので,光 :1,の割合で時を刻むので,光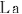 が が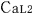 と と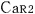 に到着するのに要する時間差 に到着するのに要する時間差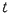 を を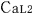 と と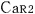 の時刻から の時刻から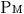 が読み取ると, が読み取ると,
|
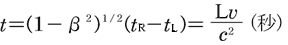
|
(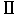 3) 3)
|
|
|
つまり,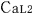 は は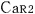 より, より,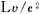 (秒)進んでいる.( (秒)進んでいる.(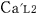 と と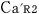 の時間差についても同様) の時間差についても同様)
ただし,ここで注意しなければならないのは,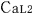 と と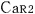 の時刻が異なっているのは,観測者 の時刻が異なっているのは,観測者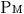 から観測した場合である.ロケットa内の観測者 から観測した場合である.ロケットa内の観測者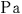 にとっては,これら2つの時計は同時刻であり,このままでは, にとっては,これら2つの時計は同時刻であり,このままでは,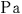 が2つの時計の時刻の絶対的時間差など論ずることはできない. が2つの時計の時刻の絶対的時間差など論ずることはできない.
そこで,次の操作として,通常は一致していない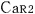 の時刻を の時刻を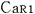 の時刻と一致させるために,ある時間調整 の時刻と一致させるために,ある時間調整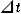 を行ない,これと同じ時間調整をさらに を行ない,これと同じ時間調整をさらに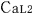 に対しても行なったとする.(勿論,実際に時計を操作して時刻を一致させる必要はなく,計算上の調整でかまわない) に対しても行なったとする.(勿論,実際に時計を操作して時刻を一致させる必要はなく,計算上の調整でかまわない)
この状況を天体Mの観測者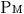 が観測すると,ロケットa内の前方の が観測すると,ロケットa内の前方の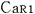 , ,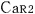 と後方の と後方の は,時刻が一致していて, は,時刻が一致していて,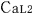 だけが, だけが,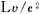 (秒)進んでいることになる. (秒)進んでいることになる.
従って,当然のことであるが,ロケットa内の観測者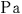 が,後方の時計, が,後方の時計, と と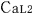 の時刻を比較した場合, の時刻を比較した場合,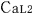 が が より, より,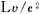 (秒)進んでいることになる.これは,特殊相対論の予測と一致する. (秒)進んでいることになる.これは,特殊相対論の予測と一致する.
また,ロケットa 内の 内の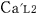 と と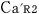 についても同様な時刻合わせと時間調整を行なった後,観測者 についても同様な時刻合わせと時間調整を行なった後,観測者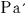 が後方の時計, が後方の時計,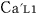 と と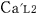 の時刻を比較すると, の時刻を比較すると,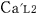 が が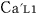 より, より,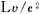 (秒)進んでいる. (秒)進んでいる.
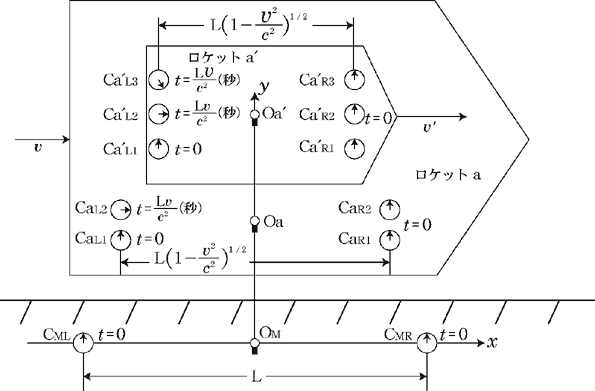
さて,次はロケットa内でロケットa が速度 が速度  で等速度運動を始めた時に, で等速度運動を始めた時に, 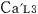 と と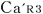 の時刻合わせを行なう.(図4参照) の時刻合わせを行なう.(図4参照)
|
 |
|
天体M「絶対静止系」
|
|
図4.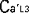 と と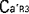 の時刻合わせ. の時刻合わせ.
|
|
この図では,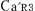 の時刻を の時刻を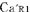 の時刻と一致させるために必要な時間調整を の時刻と一致させるために必要な時間調整を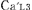 にも同様に行なっている. この時, にも同様に行なっている. この時,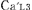 は は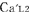 より より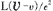 (秒)進んでいるが,これは特殊相対論の予測する (秒)進んでいるが,これは特殊相対論の予測する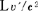 (秒)とは異なっている.[ただし, (秒)とは異なっている.[ただし,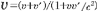 ] ]
|
|
いま,観測者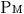 が測定したロケットa が測定したロケットa の速度を の速度を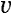 として, として,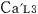 と と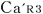 の時間差 の時間差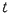  を を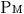 から観測すると,いままでの考察より明らかなように, から観測すると,いままでの考察より明らかなように,
|
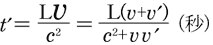
|
(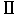 4) 4)
|
|
|
[ただし,相対論より,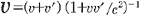 ] ]
|
|
そこで,次の操作として,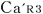 の時刻を の時刻を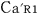 と と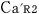 の時刻に一致させるためにある時間調整 の時刻に一致させるためにある時間調整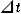  を行ない,これと同じ時間調整をさらに を行ない,これと同じ時間調整をさらに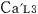 に対しても行なう. に対しても行なう.
この状況を天体Mの観測者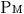 が観測すると,ロケットa が観測すると,ロケットa 内の前方の 内の前方の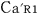 , , 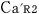 , , 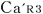 と後方の と後方の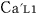 は時刻が一致するが, は時刻が一致するが,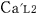 は,これら4個の時計より, は,これら4個の時計より, 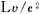 (秒),また, (秒),また,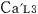 は, は,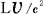 (秒)進んでいる. (秒)進んでいる.
従って,ロケットa 内の観測者 内の観測者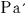 が, が,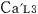 と と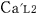 の時刻を比較した場合, の時刻を比較した場合, 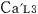 が が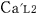 より進んでいる時間は, より進んでいる時間は,
|
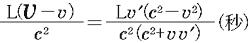
|
(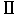 5) 5)
|
|
|
この結果は,特殊相対論の予測と矛盾する.
特殊相対論を構築する際に用いた「相対性原理」の仮定によれば,お互いに相対運動をしている慣性系は同等であるから,物理法則はあらゆる慣性系で同じでなければならない.
従って,天体Mの上空を速度 で等速度運動するロケットa内の2個の時計, で等速度運動するロケットa内の2個の時計, と と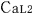 の時間差が,観測者 の時間差が,観測者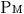 と と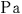 の測定で, の測定で,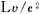 (秒)ならば,ロケットa内を速度 (秒)ならば,ロケットa内を速度  で等速度運動するロケットa で等速度運動するロケットa 内の2個の時計 内の2個の時計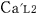 と と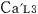 の時間差は,観測者 の時間差は,観測者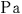 と と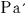 の測定で, の測定で,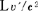 (秒)でなければならない. (秒)でなければならない.
しかし,本論の思考実験によれば,そのような結果は得られない.
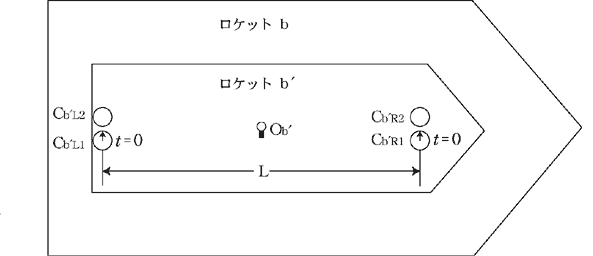
ところで,図1bのロケットb内にあるロケットb 内の4個の時計, 内の4個の時計,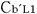 , ,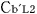 , ,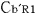 , ,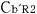 ( (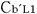 , ,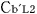 と と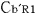 , ,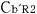 の距離はLで,中央には光源 の距離はLで,中央には光源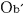 が置いてある)を使って,時刻を合わせた場合はどうか.(図5参照) が置いてある)を使って,時刻を合わせた場合はどうか.(図5参照)
|
|
|
図5.図1bのロケットb内でロケットb′が静止している.
|
|
この状態で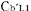 と と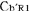 の時刻を合わせると2個の時計は,絶対的な意味で合っている. の時刻を合わせると2個の時計は,絶対的な意味で合っている.
|
|
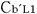 と と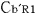 は,ロケットb内にロケットb は,ロケットb内にロケットb が静止していた状態で時刻を合わせたものである. が静止していた状態で時刻を合わせたものである.
この場合,ロケットb 内の光源から放出された光 内の光源から放出された光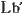 は,ア・プリオリに等方的に伝播するから, は,ア・プリオリに等方的に伝播するから,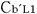 と と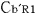 は絶対的な意味で合っているといえる. は絶対的な意味で合っているといえる.
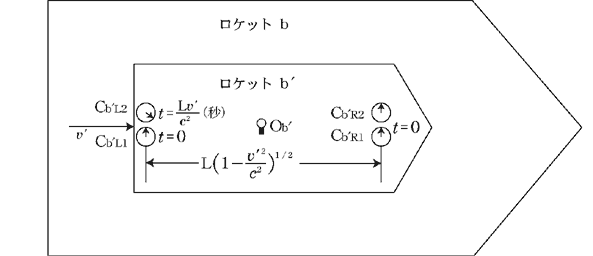
次に,ロケットb内を速度  で等速度運動するロケットb で等速度運動するロケットb 内で 内で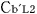 と と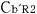 の時刻を合わせるものとする.(図6参照) の時刻を合わせるものとする.(図6参照)
|
|
|
図6.図1bのロケットb内を ′の速度で等速度運動するロケットb'. ′の速度で等速度運動するロケットb'.
|
|
この状態で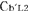 と と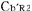 の時刻を合わせ,さらに, の時刻を合わせ,さらに,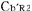 の時刻を の時刻を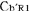 の時刻と一致させるために必要な時間調整を の時刻と一致させるために必要な時間調整を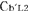 にも同様に行なう. にも同様に行なう.
この時,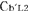 は は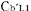 より より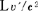 (秒)進んでいるが,これは特殊相対論の予測と一致する. (秒)進んでいるが,これは特殊相対論の予測と一致する.
|
|
この2つの時計の時間差をロケットb内の観測者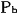 が読み取ると,いままでの考察より明らかなように, が読み取ると,いままでの考察より明らかなように,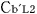 は は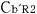 より, より,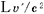 (秒)進んでいることになる.そこで, (秒)進んでいることになる.そこで,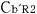 の時刻と の時刻と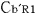 の時刻を一致させるために,ある時間調整 の時刻を一致させるために,ある時間調整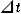 ″を行ない,これと同じ時間調整をさらに ″を行ない,これと同じ時間調整をさらに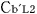 に対しても行なう. に対しても行なう.
この状況をロケットb内の観測者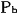 が観測すると,前方の が観測すると,前方の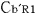 , ,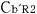 と後方の と後方の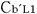 の時刻が一致していて, の時刻が一致していて,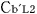 だけが, だけが,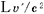 (秒)進んでいることになる. (秒)進んでいることになる.
従って,これも当然のことであるが,ロケットb 内の観測者 内の観測者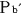 が,後方の が,後方の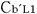 と と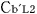 の時刻を比較した場合, の時刻を比較した場合,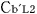 が が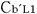 より, より,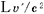 (秒)進んでいることになる.これは,特殊相対論の予測と一致する. (秒)進んでいることになる.これは,特殊相対論の予測と一致する.
しかし,同じ方法で時刻を比較したロケットa 内の時計 内の時計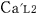 と と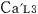 の時間差,( の時間差,(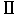 5)とは異なっている. 5)とは異なっている.
以上の議論より,ロケットa 内の4個の時計( 内の4個の時計(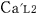 , ,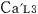 , ,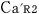 , ,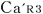 )とそれに対応するロケットb )とそれに対応するロケットb 内の4個の時計( 内の4個の時計(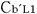 , ,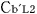 , ,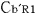 , ,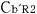 )の対比は次のようになる.(以下は図4と図6の説明) )の対比は次のようになる.(以下は図4と図6の説明)
|
|
|
ロケットa′内の時計(図4)
左側(後方) 右側(前方)
|
|
|
|
|
|
(ロケットa内の空間は、深層速度ベクトル を持つ) を持つ)
|
|
ロケットb′内の時計(図6)
左側(後方) 右側(前方)
|
|
|
|
|
|
(ロケットb内の空間には,深層速度ベクトルは存在しない)
|
|
|
さて,以上の思考実験により,図1aにおけるロケットaと図1bにおけるロケットbの内部の空間の物理的状態の相違を検出する方法を提示できた.
ところで,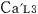 と と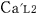 の時間差( の時間差(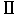 5)が特殊相対論の予測と一致しなかった原因を何に求めたら良いか.その原因を説明するためには,ロケットa内の空間が,何らかの基準系に対して,“ある速度 5)が特殊相対論の予測と一致しなかった原因を何に求めたら良いか.その原因を説明するためには,ロケットa内の空間が,何らかの基準系に対して,“ある速度 ”で運動していると考えれば良い. ”で運動していると考えれば良い.
しかし,現実の物理空間には,「絶対静止系」など存在しない訳だから,“ある速度”をそのような基準系に対する速度と考えることはできない.
そこで,本論は,空間は重層構造を持つと想定する.
つまり,真空を1つの層と考え,現実の物理空間を別の層と考え,真空上の各点に想像上の静止空間(深層静止空間)を考える.
そして,光の伝播が異方的と考えられるロケットa内の空間は,深層静止空間に対して速度 で運動していると考える.このような時,ロケットa内の空間は,深層速度ベクトル で運動していると考える.このような時,ロケットa内の空間は,深層速度ベクトル を持つと定義する.[注] を持つと定義する.[注]
一方,光の伝播が等方的と考えられるロケットb内の空間には,深層速度ベクトルは存在しない.
ただし,深層静止空間は実在の空間ではない.質量による“空間の引きずり効果の程度”を深層速度ベクトルという未知の物理量の大きさによって記述するために導入された,想像上の空間である.(ただし,“空間の引きずり効果の程度”をベクトル表示した場合,深層速度ベクトルとベクトルの大きさは等しいが,向きは逆になる)
そして,光はこの静止空間の各点に対して等方的に伝播すると考えると,光速は光源の速度に依存しないことが理解できる.
また,深層速度ベクトルは,物理空間自体が持っている速度ベクトルではない.現実の物理空間内の点と同一座標上にある深層の真空内の静止空間(深層静止空間)を起点とし,その点と同一座標を占める物理空間を終点とするベクトルである.
さて,次はいままでの考察の中で導入された深層速度ベクトルの大きさを実際に導く.本論ではこのベクトルの大きさを特殊相対論が予測する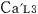 と と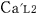 の時間差, の時間差,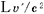 (秒)と本論思考実験2が予測した時間差,( (秒)と本論思考実験2が予測した時間差,(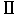 5)より導く. 5)より導く.
ただし,一般には,ベクトルの方向は明らかではないので,ここで求めるベクトルの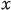 軸方向の成分を 軸方向の成分を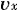 (ただし, (ただし,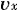 >0)とし,さらに次のような >0)とし,さらに次のような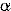 を定義する. を定義する.
|
|
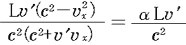
これにより,
|
(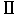 6) 6)
|
|
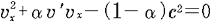
|
(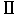 7) 7)
|
|

|
(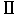 8) 8)
|
|
|
しかし,ここで問題にしているのは,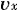 >0の場合であるから,マイナスの解を削除すると, >0の場合であるから,マイナスの解を削除すると,
|
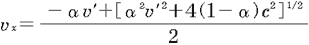
|
(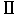 9) 9)
|
|
|
以上で,深層速度ベクトルの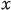 軸方向の成分を求めることができた. 軸方向の成分を求めることができた.
さらに,同様な実験を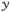 軸, 軸,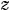 軸方向についてくり返すことにより, 軸方向についてくり返すことにより,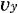 , ,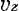 の大きさを求めることができ,これら3つの方向の成分を合成すると,深層速度ベクトルの大きさを求めることができる. の大きさを求めることができ,これら3つの方向の成分を合成すると,深層速度ベクトルの大きさを求めることができる.
|




